Read our paper on dislocation motion in crystals of colloidal peanuts.
Colloidal suspensions are thermal systems consisting of solid, traditionally spherical particles suspended in a liquid solvent. The colloidal particles can be large - on the scale of one micron - making them big and slow enough to observe with an optical microscope. As such, colloids offer a truly unique opportunity to actually watch the time evolution of a thermodynamic system, particle by particle. While the spherical particle is a reasonable choice for representing an “atomic unit", recent advances in particle synthesis techniques have enabled the production of many new, exotic anisotropic particles. We have explored phases formed by hollow, fluorescent, peanut-shaped silica particles. These colloidal peanut particles are made up of spherical lobes of diameter 1.36 microns and lobe separation 1.46 microns. The suspension of particles is pipetted into a sealed wedge-shaped cell, and particle area fraction is controlled by tilting the cell so that particles sediment into the viewing region, which accommodates a monolayer of particles. The particles are then observed using a confocal microscope.
The particles form "Degenerate Crystals" in which the particle lobes occupy triangular lattice sites while the particles are randomly oriented among the three crystalline directions. Now, in some ways, this Degenerate Crystal (DC) phase sounds very reminiscent of the familiar system of close-packed spheres. However, although the two ordered phases are structurally similar, their dynamics are quite different. A simple thought experiment highlights some of these differences: consider a crystal of close-packed spheres and a DC, both under shear along one of the crystalline directions, as shown below. The crystal of spheres can relieve the stress by slipping, so that the spheres of one row slide along the spheres of the next row. However, if you just blindly apply the same deformation to the DC, some of the peanut bonds would have to be broken. This means that certain particle orientations (represented by the red particles) block slip.

Now, in thermodynamic systems where the energetic cost of simultaneously breaking all the bonds between two adjacent rows would be prohibitively high, slip occurs via the motion of local deformations called dislocations. These dislocations are characterized by a pair of spheres (or peanut lobes), one having five nearest neighbours and one having seven nearest neighbours . Each dislocation can only glide along one axis, the line parallel to its Burgers vector. The Burgers vector is found by drawing a Burgers circuit and recording the vector that would complete the circuit (see below).
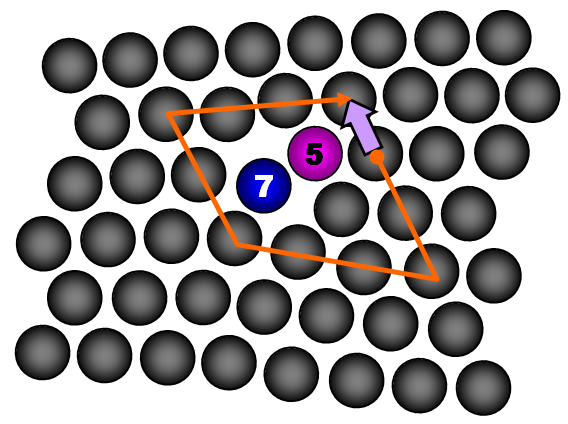
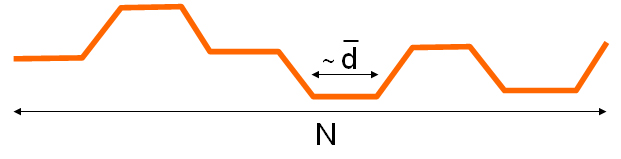
So, what all this means for DCs is that there are certain peanut particle orientations that block the glide of dislocations. If a dislocation pair forms in a DC, then each dislocation will glide along its Burgers vector direction until it encounters a “blocking” particle oriented like the red particles in the second figure. But the question is: who cares? Is this really a big deal? How often would dislocations encounter such particles anyway? To address these questions, we looked at the distribution of separation distances between blocking particles, as shown below.

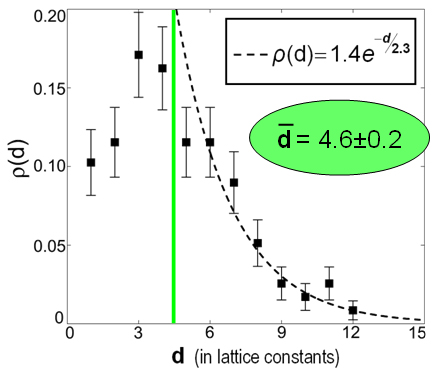
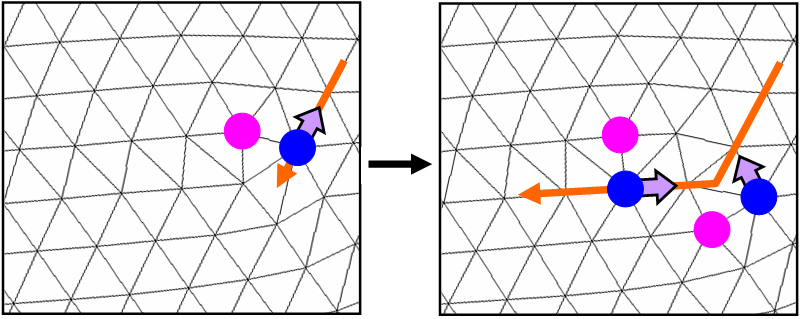
Surprisingly, the average separation d between such particles is only about 5 lattice constants! That means that dislocations are restricted to glide back and forth along very short straight segments. How then, can dislocations achieve long range transport, as is required in shearing or melting? While we still do not have a complete answer to this question, we have observed one mechanism for the dislocations to bypass blocking particles. While it’s true that dislocations can only glide along straight lines parallel to their Burgers vectors, it is possible for a dislocation to turn and travel along a different crystalline axis, if it undergoes a dislocation reaction. Below, a simple dislocation reaction in which one dislocation splits into two dislocations is pictured using images from the wonderful online applet at http://physics.syr.edu/thomson/thomsonapplet.htm, created by Cris Cecka and Mark Bowick at Syracuse University. In this sequence, a single dislocation glides down from the upper right. It then spits out and additional dislocation to the lower right and travels along a different crystalline axis towards the left. The rule for such dislocation reactions is that the net Burgers vector is conserved.
We have experimentally observed such dislocation reactions, which can be used to circumvent obstacles formed by blocking particles in the initial glide path of a dislocation (see below).
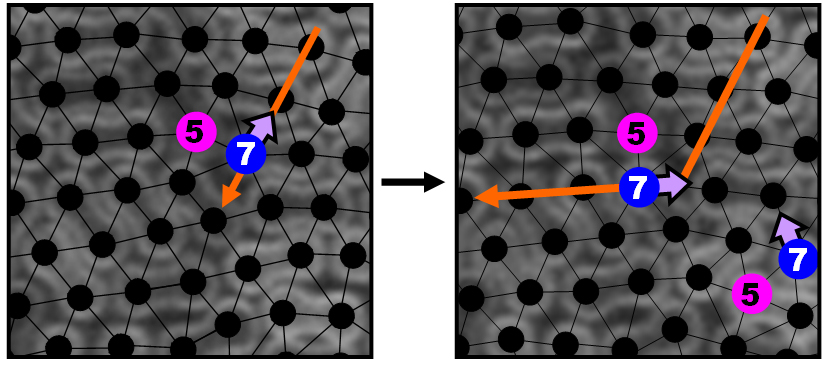
So then, one can begin to imagine a scenario in which long range dislocation transport is enabled by a sequence of such dislocation reactions. A pair of dislocations with opposing Burgers vectors can initial glide apart as they would in a crystal of spheres. Then, when each encounters an obstacle, they can undergo a reaction, spitting out a new dislocation and continuing along an available, unblocked straight segment along another crystalline axis. When once again they meet obstacles, they can again undergo reactions, and so on and so forth along a zig-zag pathway until they reach a final separation of N lattice constants (see below).
Okay, so, such a scenario could transport dislocations over arbitrarily long distances, but is it actually energetically feasible? To hear the rest of the story, please look through the powerpoint below, which is a copy of a talk presented by Sharon Gerbode at the 2008 Fall MRS Meeting in Boston.
Also, read our paper on dislocation motion in crystals of colloidal peanuts.
