Articular cartilage (AC), a biological tissue that protects and lubricates joints, plays a critical role during healthy locomotion. Ongoing work in the Cohen lab has been examining the spatially heterogeneous mechanical properties of this tissue using confocal rheology. This technique allows us to simultaneously deform the tissue with a known stress and measure the local strain field. From this information, we can calculate the local shear properties. Our early work in this field found a highly complaint region localized to the tissue's surface that is between 10 and 100 times more complaint than the bulk, which we believe is vitally important for the the tissue's normal functioning. Naturally, this observation leads to the question: What drives AC's depth-dependent shear properties? In this project, we combined mechanical testing with structural quantification to address exactly this question. Our work was published here, and below, we offer a brief overview of the main results.
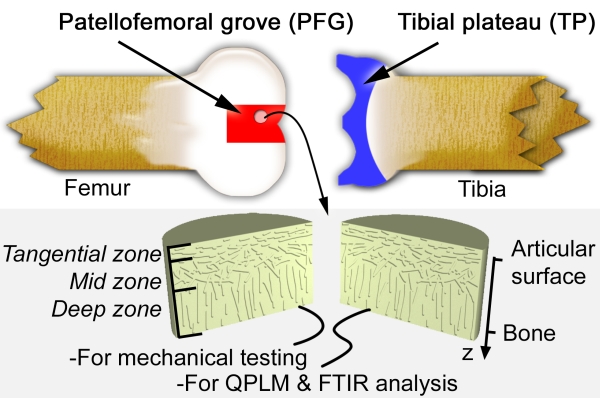
This schematic diagram of a bovine knee joint indicaties our sample harvesting sites. Cylindrical plugs of AC were removed from the joint, halved, and separated out for mechanical testing or biochemical analysis. AC is known to have three zones distinguished by collagen fiber orientation as indicated. The coordinate system used throughout this summary is also shown, where the depth-wise direction z is 0 at the surface of the tissue, and increases toward the bone.

The measured depth-dependent shear modulus for the 8 samples we tested is plotted on a log scale as a function of depth, z. Red curves are from the patellofemoral grove (PFG), while blue curves are from the tibial plateau (TP) as indicating in the figure above. The surface region highlighted in gray is found to be 10 to 100 times more compliant than the tissue at greater depths, and when compared to fiber organization (previous figure and data in paper), corresponds to AC's tangential zone.

One possibility is that the depth-dependent shear properties arise from the depth-dependent collagen architecture, which was shown in the cartoon sketch above. To test this hypothesis, we used quantitative polarized light microscopy to measure alignment of collagen fibers in the tissue. The data, however, shows no particular correlation between fiber organization and shear properties. An alternative hypothesis is that the collagen matrix density drives the observed depth-dependent behaviors. This figure shows (A) Fourier transformed infread imaging (FTIR-I) data that examines the depth-dependent (B) aggrecan volume fraction, va, and collagen volume fraction, vc. (C,D) When plotted against the shear modulus, we find a remarkable correlation that gives a structure-function relation of the form G ~ (vc - v0)p. In this expression, v0 is a constant determined by the fits and the exponent p is greater than 1. This functional form suggests a non-tivial relationship between the microscopic architecture and macroscopic properties that can not be reduced to simple continuum elasticity.

To better understand the experimental data, we model collagen fibers in AC as a 2D network of elastic fibers connected on a disordered kagome lattice and embedded in an elastic medium. (A) The fibers have linearly elastic stretching and bending moduli, as does the embedding medium. In this figure, continuous black lines constitute fibers while light gray lines are missing bonds. In simulations, we vary the fiber volume fraction, vf, by removing bonds, which ultimately leads to a critical percolation transtion when the network no longer contains a spanning connected cluster. Calculations of the networks shear modulus as a function of elastic moduli are carried out by applying external loading in the simulation, minimizing the system's energy, and examining the overall strain. Zooming in on the sheared lattice, we find affine deformations where light and dark colored bonds overlap, and non-affine deformations where they do not. Schematic diagrams illustrate the various energetic contributions included in the model described by Eq.(1) in the manuscript. (B) In the absence of a reinforcing medium, the four distinct regimes of the model corresponding to the four points labeled I - IV in panel (C) are schematically illustrated. In the presence of a reinforcing medium, such as points V and VI in (D), the strength of the reinforcing medium modulus can be schematically illustrated by shading the background. (C) Exploring the model's dependence on the fiber bending-to-stretching modulus ratio in the absence of a supporting medium reveals a rigidity percolation phase transition as a function of vf. (D) In the presence of a supporting medium, the phase transition is broadened, and G(vf) becomes dominated at low vf by the modulus of the reinforcing medium. All modulus curves are normalized by the value of a fully connected lattice. Collectively, the model has 2 parameters constructed from the ratios of three elastic moduli and is capable of producing structure-function correlations similar to those seen in our experimental data. The goal therefore is to fit the model to the data and see whether the predicted model parameters are biophysically plausible.

(A) Using experimentally measured wet volume fraction data from sample PFG 1, we generated a kagome lattice that is random and isotropic along the direction of shear, but has a varying density of bonds along the z axis. Zoomed insets show the region near the articular surface is below the percolation threshold, while the region at greater z is more well connected. For each inset, the largest percolating cluster is colored red, while the remaining network is colored black. In regions below the percolation threshold, stresses are transmitted by the supporting background medium. (B) For specific model parameters, a comparison between experiment (light gray points) and simulation (dark gray points) show reasonable agreement. The shear modulus is decomposed into contributions from the reinforced fiber network (dashed blue) and the reinforcing medium (solid blue). For low vf, the fiber network does not percolate across the system and the reinforcing medium dominates. At the critical connectivity threshold, the fiber network forms a spanning cluster and stresses can be transmitted across the system. This effect rapidly dominates with increasing vf, but becomes less sensitive at higher volume fractions. (C) The spatially homogeneous vf is replaced with experimentally measured vc(z) from sample PFG 1 to generate a depth-dependent G(z) profile (red), which when superimposed on experimental data (light gray lines) show qualitatively similar behavior.
Overall, this project makes exciting headway toward an understanding of AC's shear properties. It goes beyond the well-established poroelastic theory of cartilage by offering a microscopic description of the structure-function relationship, which is typically treated on a purely phenomenological basis with viscoelastic constitutive relations. Indeed, a publication released by our collaborators in the Bonassar lab (Griffin et. al., J. Ortho. Res., 2014) provides an orthogonal set of measurements that support the ideas proposed here, and contributes to this new direction in cartilage mechanics.
This work was published in Biophysical Journal 107(7), 2014 and featured as the cover article as well as in the Biophysical Society Blog!

