How insects recover from aerial stumbles
How do insects solve the problem of keeping stable in the face of unpredictable disturbances, such as gusts of wind? We devised a way to study insect flight control and stability by experimentally “tripping” insects in flight!
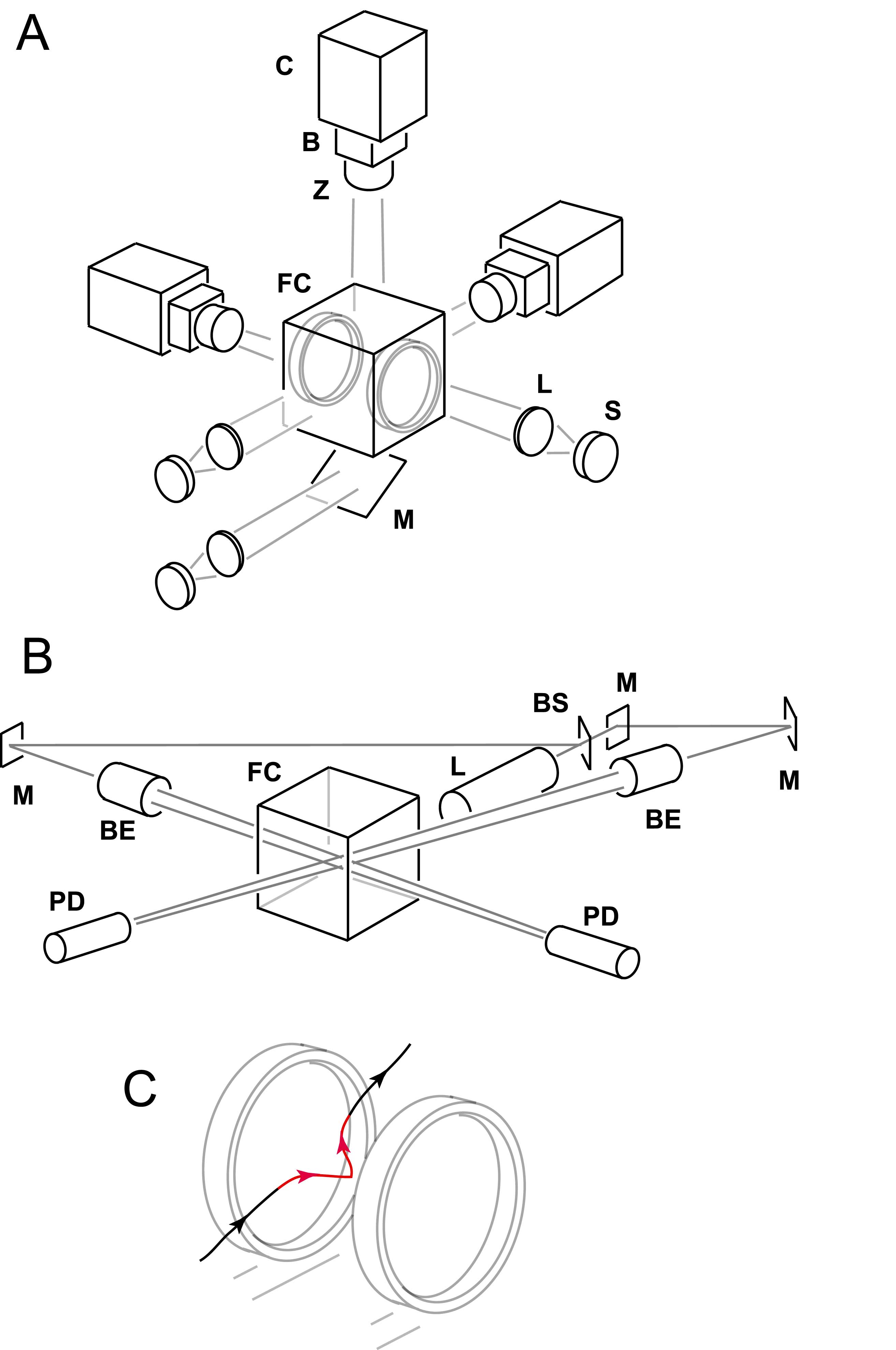
We inserted a pair of Helmholtz coils into our flight chamber and assembled a circuit that passes a brief current through coils, generating a magnetic field. We then glued tiny magnets to fruit flies. When these insects fly through the region of interest, they automatically trigger the field to turn on for one wing-beat. This field torques the insects, and we film this aerial “stumble”.
Here is a reconstruction of a perturbation experiment in which the insect flies left to right. We display video snapshots spaced by about 4 wing-beats on the side panels of this image, and the insect’s configuration is shown on a computer-generated model. The perturbing torque acts for only one wing-beat and is indicated by the red arrow. The insect is rotated to its right by 55° but then recovers its orientation by making a corrective left turn. In this case, the fly recovers its yaw angle to about 4° in about 14 wing-beats or 60 milliseconds. Impressive!
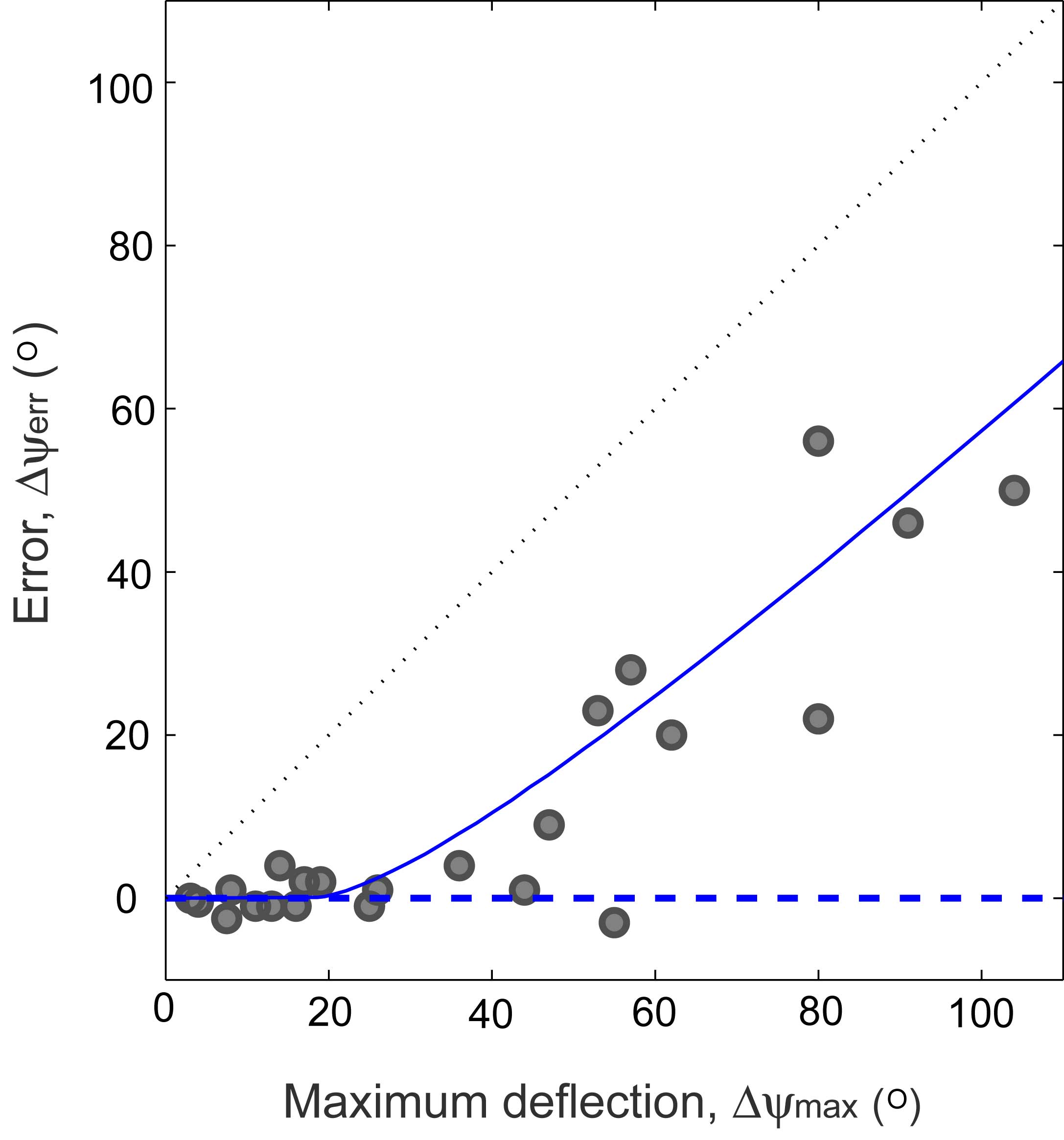
The insects are sometimes very good at recovering and sometimes not so good. Above we plot the accuracy of their recovery (final minus initial yaw angle) for increasing strengths of the applied perturbation. For gentle perturbations, the insects recover with an accuracy of 2°, and as we induce greater deflections of the flies, this error increases. In all cases, the insects attempt to correct by adjusting their wing motions in a stereotyped way.
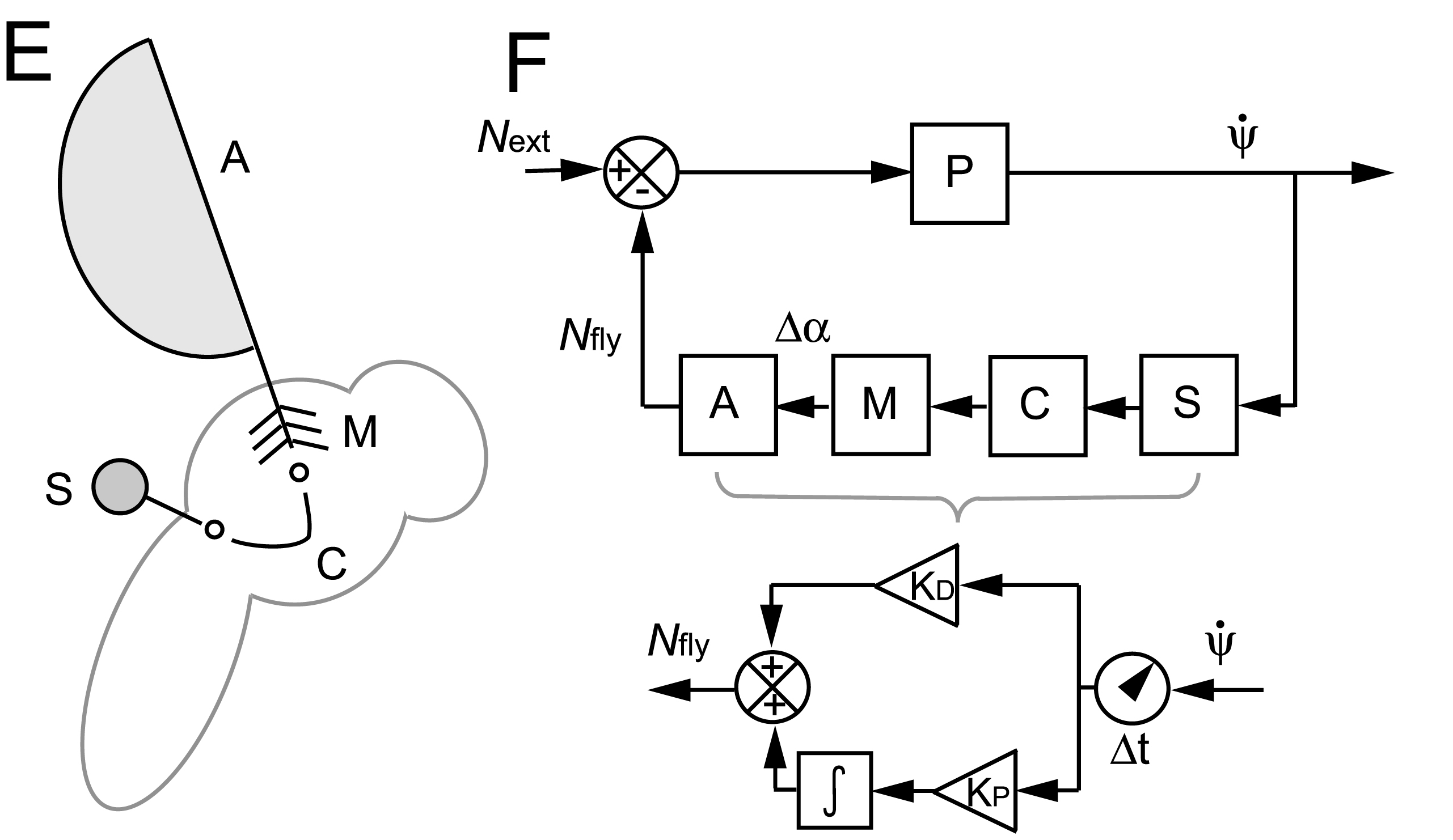
We used measurements of the insect body and wings to form a feedback model of how the insect senses its rotation, processes this information using a neural circuit, and then adjusts its wing motions accordingly.
The simplest model that is consistent with all of our data is proportional-differential (PD) controller. However, this model alone guarantees perfect correction. To account for imperfect correction, we modified the PD model to include the effect of sensor saturation. This nonlinear model gives the blue solid curve in the error plot that is consistent with all of our observations.